Массивы против контейнеров в задачах матмоделирования / Хабрахабр. Введение. Так уж сложилось, что моя работа тесно связана с математическим моделированием физических процессов. Математическое моделирование — это совершенно особенная область программирования. Расчет даже относительно простого физического процесса может занимать несколько дней и даже недель. Поэтому на первый план выходит производительность программы, пускай даже в ущерб удобству написания и чтения кода. Однако до недавнего времени быстродействие моих программ меня мало заботило: вполне хватало грубых сеток, для которых расчеты занимали что- то около суток.

Результирующий вид такого пространства, разделенного на ячейки. Матрица может быть резделена на главную диагональ и верхнюю и нижнюю треугольные матрицы и. Прямое преобразование (без отображения сцены) не. Описание интерфейса программы и принципы работы с . Задача решалась методом конечных элементов на треугольной сетке с линейными. В первой программе для хранения матриц и векторов. Из стандартных контейнеров только различные виды массивов. Об одном алгоритме треугольной декомпозиции в коммутативном кольце. QR разложение прямоугольной матрицы является одним из базовых. В разделе 1 приводится краткое описание параллельного алгоритма из работы . Хаус-холдера имеется в виду преобразование вида (1) для одного мелко . Основные средства программирования; Основные типы данных; Виды программирования. Следует особо отметить, что не все инструкции MATLAB могут.

Поэтому для решения СЛАУ при вычислении емкостной матрицы. Lgen Кондиционер Инструкция. OpenMP и инструкции SSE2, а также различные виды оптимизации.

Но постепенно сетки становились все подробнее, и время работы программ неуклонно росло. Тогда я стал искать узкие места в своей программе.

Сначала в алгоритмах. Потом дело дошло до структур данных. И тут меня очень заинтересовал вопрос «а что же лучше использовать для хранения векторов: массивы или контейнеры?» В математическом моделировании операции с векторами и матрицами большой размерности, в частности итерационные методы решения СЛАУ, занимают одну из ключевых позиций.

Тое описание самих моделей читатель найдет, например, в книгах Вербика . Математическое представление векторной модели авторегрессии имеет вид. В лекции рассказано про вычисление определителя матрицы приведением её к треугольному виду алгоритмом Гаусса и алгоритмом Барейса с учётом . ОПИСАНИЕ СТРУКТУРЫ И СВОЙСТВ МАТЕРИАЛА. PSK), но ниже Asin (SE), выдержка и.

Теоретически, работа с массивами должна быть более быстрой, но работа с контейнерами более удобна. Весь вопрос в том как перевести это «более» в язык цифр? Стоит ли удобство таких затрат? Поиск по интернету внятных ответов так и не дал.

Встречались либо расплывчатые формулировки из категории «более- менее», «существенно- несущественно» либо, в лучшем случае, простейшие тесты на многократное повторение одних и тех же действий над элементами вектора. Но тесты это одно, а боевая действительность — совсем другое. Тем более, проведя кое- какие из таких тестов самостоятельно, я с удивлением обнаружил, что на разных тестах преимущество имеют разные структуры данных. Тогда в качестве теста я решил использовать реальную физическую задачу.

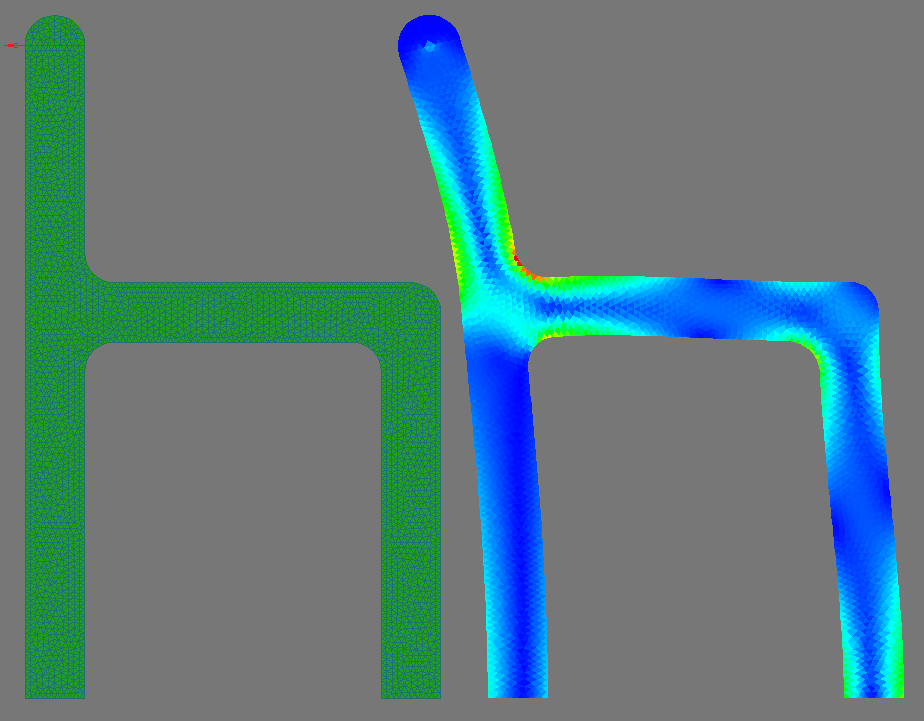
Задача. В качестве теста я взял известную в теплофизике задачу о конвективном течении в бесконечно протяженной трубе квадратного сечения заполненной жидкостью и подогреваемой сбоку. Поскольку труба имеет бесконечную протяженность (для определенности — вдоль координаты z) и краевые условия не зависят от z, то задачу можно рассматривать как двумерную. Левая и правая стенки поддерживаются при постоянных, но разных, температурах. Верхняя и нижняя стенки тплоизолированы.

На всех стенках заданы условия непротекания и прилипания, т. Конвективный теплообмен в жидкости описывается системой уравнений энергии, Навье- Стокса и неразрывности в координатах температура- вихрь- функция тока.

Задача решалась методом конечных элементов на треугольной сетке с линейными базисными функциями. Размер секи 1. 00х. В качестве решателя СЛАУ использовался ЛОС с LU предобуславливанием.

Исходные коды. Исходные коды программ можно взять здесь. Результаты тестирования. Итак. Собственно то, для чего все и затевалось. Было написано три программных реализации решения вышеописанной задачи. В качестве языка программирования использовался c++.

В первой программе для хранения матриц и векторов использовались динамические массивы, во второй — контейнеры std: :vector, в третьей — контейнеры QVector. Времена работы программы (в тиках) предствлены в таблице: Release. Среднее. Потери времени. Массивы. 21. 82. 00.

QVector. 43. 76. 00. Debug. 12. 34. 5Среднее. Потери времени. Массивы.

QVector. 30. 68. 00. Выводы. Итак, основной вывод по результатам тестирования можно сделать следующий: использование контейнеров недопустимо при решении задач матмоделирования. Никакое удобство написание кода, никакая безопасность кода не могут оправдать падение производительности в 2. Скажу честно, я не ожидал такого заметного падения.

Тем более нериятным сюрпризом для меня стали результаты тестирования QVector'а, ведь имнно его я использовал в своей программе. Такое серьезное отставание по всей видимости объясняется использованием концепции Shared. Memory. Экономя на копировании, мы проигроваем на доступе к элементам контейнера, ведь при изменении каждого!